The Circle of 5ths is an extremely important element of music theory and has many uses, mainly in understanding how keys and chord changes work and are put together. But first, what is a 5th?
A 5th, or “perfect 5th,” is an interval. Intervals measure the distances between notes. Quite simply, it’s the distance between the first and 5th notes of a scale. So, if our scale is C, D E F and G and we replaced those note names with numbers, C being 1, D being 2, and so on, G would be the 5th. So the distance from C to G is considered a 5th. In the same way, C up to D would be called a 2nd, C to E is called a 3rd, and C to F is a 4th.
Perfect 4ths and 5ths
Lets look at the whole scale:
C D E F G A B C
Now, consider, C up to G is a 5th, but so is D up to A (if D were 1, D E F G A equals 1, 2 3 4 and 5), E up to B. and from G up to C is a 4th. Notice from G up to the C the distance would be a 4th. So, from C up to G is a 5th, from G up to C again is a 4th. We could say C up to G is an “ascending 5th” while C down to G is a “descending 4th.”
The Science of Why 4ths and 5ths Sound Right
Okay, sorry in advance if this next part gets tedious. You can skip it if you like.
Middle C has a frequency of 261.63 hertz, or 261.63 cycles per second. We’re going to cheat and round it off to 260, just to make the math a little easier. If we start our scale at middle C, then the C at the top of the scale is exactly double the frequency. So, 261.63 for middle C and 523.26 for the C an octave up, Octave being an “8th” interval. Or, if since we’re cheating (imagine a guitar tuned just a tad flat), 260 for the lower C and 520 for the higher one.
There’s a reason both are called C; a reason both notes have such a similar sound to our ears. When we hear a C 260, the air is vibrating 260 times a second, and causes our eardrum to vibrate at that same frequency. If we hear 260 and 520 at the same time, imagine one part of your eardrum moving 260 times a second (i know it’s not that simple, but it’s easier to visualize) and the other part moving at 520 times a second. So, half the time the parts of the eardrum are moving in the same direction. The ratio between these 2 notes is 1:2 and an octave is the most harmonious or consonant combination of notes possible.
In this way, notes that have a low ratio sound more consonant, and those with a high ratio (the vibrations will coincide much less often) have a more dissonant sound to us. The ratio of C to G (260 to 390), the Perfect 5th, is 2:3 and then from G up to the higher C (390 to 520), the Perfect 4th, is 3:4. These combinations of notes still sound very consonant to us.
The Good News
The good news is, we don’t have to do all these calculations, or even know these frequencies and ratios. All we need to do is memorize the Circle of 5ths.
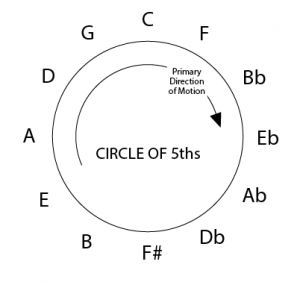
I’ve written the above circle backwards from what is commonly seen because I wanted the primary direction of motion, descending fifths, to be clockwise. Clockwise on this circle are descending 5ths (or ascending 4ths) and counter-clockwise is ascending 5ths (descending 4ths).
The Circle and Chords
The Circle of 5ths is the sequence of all notes that are a 5th (or 4th – remember moving up a 5th or down a 4th are the same thing) apart. In the same way the notes played together sound harmonious, chords that are adjacent in the Circle sound really “right” with one another. Going from a C major chord to a G major, F to C, and so on, just sound natural.
It’s a good idea to play through the Circle using chords, listening to how they sound, memorizing the order of the names of the chords. In time, you’l be able to distinguish the sound of chords moving in 4ths and 5ths, and later, you’ll be able to distinguish the sounds of chords that are 2, 3, 4 or more tones away in the Circle.
The Circle in a Key
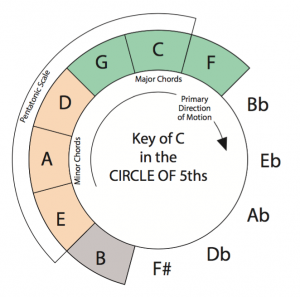
Lets look at the notes of the Key of C in the context of the Circle.
The notes of the C Major Scale are
C D E F G A B C
and would be numbered
1 2 3 4 5 6 7 1
(8 being C, the octave)
Looking at the Circle, you’ll notice these 7 notes are all grouped together. the C, F and G are the 1st, 4th, and 5th tones of the scale. They are adjacent in the Circle and are the 3 major chords of the key. Next to these are the 3rd, 6th and 2nd tones of the scale. These are the 3 minor chords of the key. Lastly, the B, or 7th tone, is the only diminished chord in the key of C Major.
If we rearranged the scale so that we were moving in defending fifths the order would be
1 4 7 3 6 2 5 1
But, since we’re talking about chords instead of notes, lets use Roman numerals, and we can use upper case for Major, and lower case for Minor and diminished, adding a º symbol to denote the diminished chord:
I IV viiº iii vi ii V I
C major is the tone center of this key, and A minor is the relative minor tone center.